  
Next: Recursive Implementation of General
Up: Recursive Windowing of Time
Previous: Recursive Windowing of Time
Windowing a time series 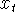 means computing another time series means computing another time series 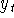 by the formula
by the formula
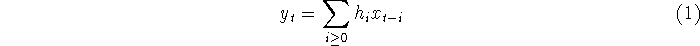
where the numbers 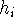 define the window. In the case where the
input series define the window. In the case where the
input series 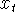 is a unit impulse is a unit impulse
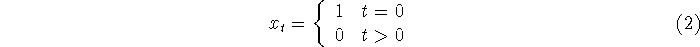
the output time series 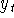 is called the impulse response of the
windowing filter. Alternatively, we can obtain the series is called the impulse response of the
windowing filter. Alternatively, we can obtain the series 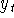 by passing by passing
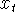 through any filter with the same impulse response. Different filters
with the same impulse response are called different realizations of
each other. Although all realizations of the a filter have the same signal
characteristics, not all realizations of the same filter have the same
properties when approximated by finite precision (fixed or floating point)
arithmetic, and not all realizations require the same amount of
computational cycles. This note explains how to obtain particularly
advantageous realizations. through any filter with the same impulse response. Different filters
with the same impulse response are called different realizations of
each other. Although all realizations of the a filter have the same signal
characteristics, not all realizations of the same filter have the same
properties when approximated by finite precision (fixed or floating point)
arithmetic, and not all realizations require the same amount of
computational cycles. This note explains how to obtain particularly
advantageous realizations.
One practical difficulty in using the representation (1)
is that it requires storage of all the values of 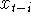 for which for which 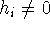 , and when used sequentially, in storage of all the values of , and when used sequentially, in storage of all the values of 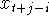 for which for which 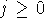 and and 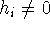 . In particular, it is not
practical to realize an IIR (infinite impulse response) filter in this way. . In particular, it is not
practical to realize an IIR (infinite impulse response) filter in this way.
The most common IIR impulse response used for windowing is the case
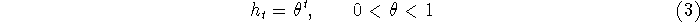
which admits the recursive realization
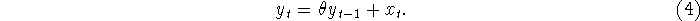
It is frequently useful to refer to the DC gain of the filter, which
is the sum of the impulse response. In this case, the DC gain is
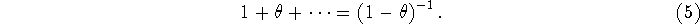
Another filter which is used for windowing is the `modified Barnwell' window
suggested by Strobach. This second order filter generalizes (4) is
given by
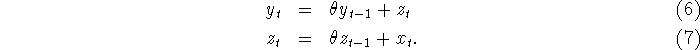
The impulse response of this window is
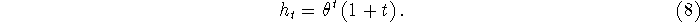
It is a little easier to see this if we recast the filter in the state
space form
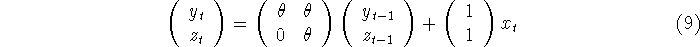
so that the impulse response is
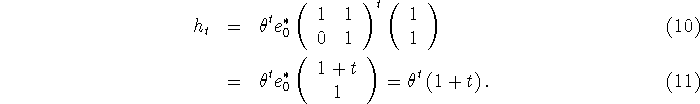
Note that we are numbering the indices of the vector starting at 0, hence
the first standard basis vector is 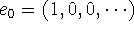 , etc. , etc.
The DC gain is
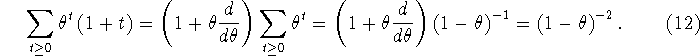
  
Next: Recursive Implementation of General
Up: Recursive Windowing of Time
Previous: Recursive Windowing of Time
Fri Jun 27 03:10:38 EDT 1997
|