  
Next: Triangular Input Balanced Realizations
Up: Maximally Flat Impulse Response
Previous: Properties of the Maximally
The rectangular window of length T has impulse response 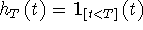 , that is , that is
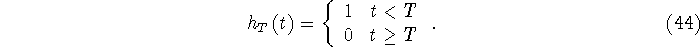
The transfer function of is
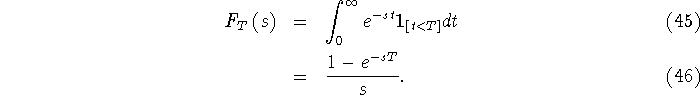
We would like to approximate a rectangular window with a maximally flat
window which means choosing 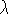 and d appropriately. The
complication is that the values of and d appropriately. The
complication is that the values of
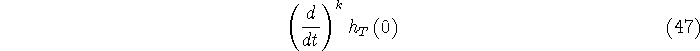
is independent of T, but our derivation of the maximally flat impulse
response only uses information local to t=0, so it cannot determine T
from this information.
One approach is to match the  moments of the functions moments of the functions 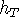 and and 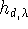 , ,
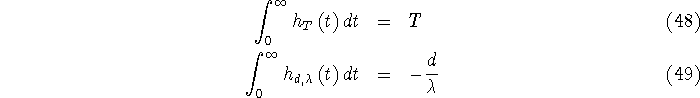
where we impose
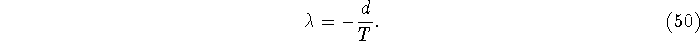
Observe that since
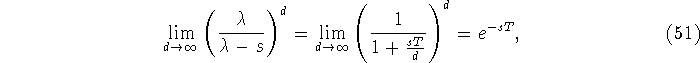
we must have
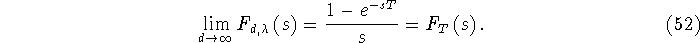
Appealing to a rather technical theory, we find that this means that
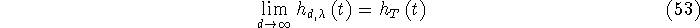
at all points of continuity of 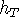 , (i.e. everywhere except for at t=T). , (i.e. everywhere except for at t=T).
This approach successfully determines T from 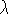 and d, but there
is still one free parameter if only T is given. When we compare higher
moments of the functions and d, but there
is still one free parameter if only T is given. When we compare higher
moments of the functions 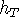 and and 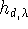 we find we find
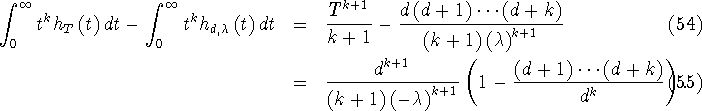
We can evaluate the term
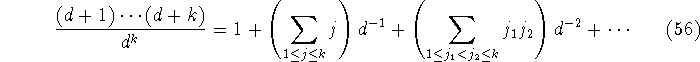
by means of the Stirling numbers of the first kind, giving
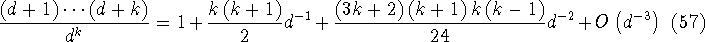
so the relative error of the 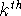 moment is moment is 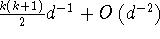 , and in particular the first moment has
relative error , and in particular the first moment has
relative error 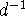 . Note that when k>0, the . Note that when k>0, the 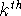 moment of moment of 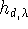 is greater than that of is greater than that of 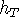 , and for k=1 this means
that the maximally flat impulse response uses older data than a
corresponding rectangular window. It also shows that no choice of d will
match higher moments than another choice. , and for k=1 this means
that the maximally flat impulse response uses older data than a
corresponding rectangular window. It also shows that no choice of d will
match higher moments than another choice.
We can also use this comparison of moments to determine how large d needs
to be for 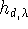 to approximate to approximate 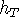 to a specified degree. to a specified degree.
Fri Jun 27 03:10:38 EDT 1997
|