  
Next: Meixner Functions and TIB
Up: Recursive Windowing of Time
Previous: Comparison With a Rectangular
In a realization of the state space form
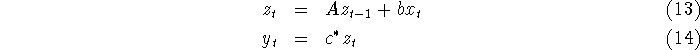
the impulse response
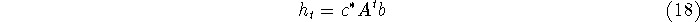
is preserved by the action
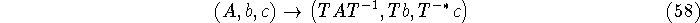
that is,
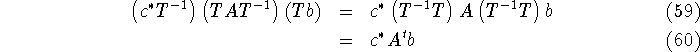
where T is a nonsingular 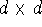 matrix. This corresponds to the
change of coordinates of the state vector matrix. This corresponds to the
change of coordinates of the state vector
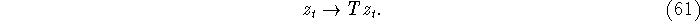
When we choose the filter parameters 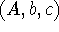 we can exploit
this symmetry to obtain choices which, although having the same signal
properties, have superior numerical or computational properties. Since these
realizations have the same impulse response, they are called observationally equivalent. we can exploit
this symmetry to obtain choices which, although having the same signal
properties, have superior numerical or computational properties. Since these
realizations have the same impulse response, they are called observationally equivalent.
After imposing some more or less unobjectionable constraints on the filter,
it turns out that any two observationally equivalent systems are related by
this type of coordinate change. Note: we should go into minimality,
observability and reachability in somewhat more detail here.
A system of dimension d is called minimal if it is not possible to
realize the impulse response with a system of lower dimension. This means
that each component of 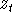 actually is used at some point, and that the
distribution of actually is used at some point, and that the
distribution of 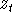 vectors actually fills up d-dimensions. However,
it can happen that a minimal realization of an impulse response involves
coordinates for vectors actually fills up d-dimensions. However,
it can happen that a minimal realization of an impulse response involves
coordinates for 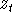 in which the vectors in which the vectors 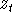 are distributed in such
a way that the variation in some directions is very small compared to
others, i.e. that the ellipsoids of constant probability are very far from
spheres. It should not be too surprising that this can expose a finite
precision realization of the system to numerical pathologies. It is
therefore desirable that all the components of are distributed in such
a way that the variation in some directions is very small compared to
others, i.e. that the ellipsoids of constant probability are very far from
spheres. It should not be too surprising that this can expose a finite
precision realization of the system to numerical pathologies. It is
therefore desirable that all the components of 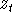 have similar
scaling. have similar
scaling.
It is impossible to obtain this property without any information about 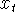 . However, if it is known that . However, if it is known that 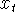 is relatively noisy, then it
is possible to get good results by choosing the coordinates for is relatively noisy, then it
is possible to get good results by choosing the coordinates for 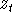 in
such a way that in
such a way that 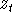 would be spherically symmetrically distributed if
the would be spherically symmetrically distributed if
the 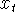 were independent and identically distributed. It turns out that
this means choosing were independent and identically distributed. It turns out that
this means choosing 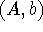 so that Stein's equation is
satisfied so that Stein's equation is
satisfied
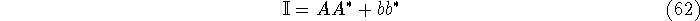
and determining c from the system
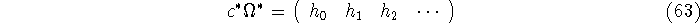
where
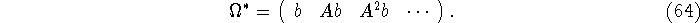
Note that
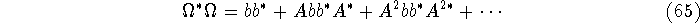
but that thanks to the Stein equation, we have
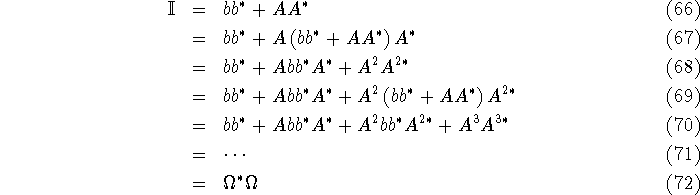
which converges as long as A is stable. (We are only interested in stable A, so we can always use this). Since
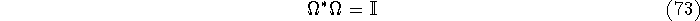
it follows that  is column unitary, and we can solve for the least
squares approximation to c by is column unitary, and we can solve for the least
squares approximation to c by
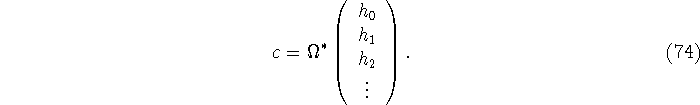
This corresponds to expanding the impulse response in the orthogonal
functions given by the columns of  , and the `Fourier' coefficients
of the impulse response are the components of c. , and the `Fourier' coefficients
of the impulse response are the components of c.
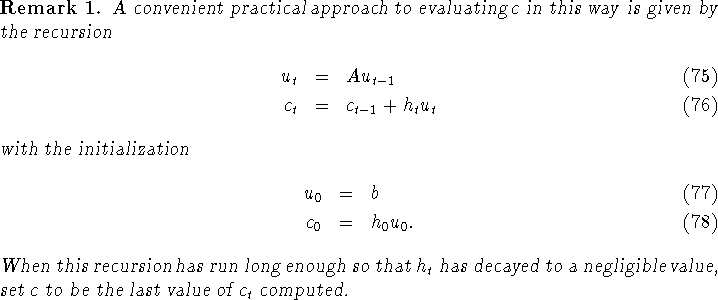
We have not exhausted the possible choices of coordinates for 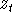 , since
by Shur's decomposition, we can always arrange for A to be triangular with
a unitary choice of T. The unitarity of T preserves the Stein equation , since
by Shur's decomposition, we can always arrange for A to be triangular with
a unitary choice of T. The unitarity of T preserves the Stein equation

and we use this choice to reduce A to a triangular matrix. A system where 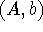 satisfy the Stein equation with A triangular is called
a Triangular Input Balanced (TIB) system. This choice is particularly
good since in addition to the good numerical properties implied by the Stein
equation, it is possible to compute satisfy the Stein equation with A triangular is called
a Triangular Input Balanced (TIB) system. This choice is particularly
good since in addition to the good numerical properties implied by the Stein
equation, it is possible to compute 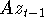 in in 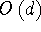 operations, as opposed to the usual
operations, as opposed to the usual 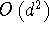 for general A. for general A.
  
Next: Meixner Functions and TIB
Up: Recursive Windowing of Time
Previous: Comparison With a Rectangular
Fri Jun 27 03:10:38 EDT 1997
|